생존분석 개요 (1.생존분석,중도절단)

최종 작성 : 2022-01-13 23:12:00

 

 

 

2019년 7월 한 달간 모 의료원에서 진행하는 암 발병 예측 프로젝트 작업에 잠깐 참여하였다.

 

사실 이 프로젝트는 3개년 간 진행되는 꽤나 큰 프로젝트이지만, 내가 직접적으로 투입된 것은 아니었기 때문에 모델생성 관련해서 자문? 알고리즘 관련 도움?을 주는 쪼꼬만 역할이었다.

 

투입 첫 주 동안은 현재까지의 진행상황 파악과 분석 방법론 파악에 힘썼다. 하지만 의학 통계 관련 지식이 일천하여 무엇 하나 제대로 이해하지 못한 것이 사실이다. 그런 상황에서 교수진과 의사들과의 미팅을 하게 되었고, 무엇인가 의견을 제시하기는커녕 내용을 받아 적기에 급급한 상황이 반복되었다. 그분들의 의학적 소견을 근거로 반론을 제기하는 상황에서 내가 할 수 있는 것은 단지 "당신들이 제공한 데이터를 분석한 결과가 이렇게 나왔을 뿐이다."라고 할 수밖에 없는 상황...

 

이런 상황들이 정말로 답답했기 때문에 내가 가지고 있는 학문적 기반을 최대한 활용할 수 있으면서 적용 범위가 상대적으로 넓은 생존분석 관련 학습을 진행하기로 결정하였다.

 

어찌 됐든 나의 학문적 기반은 수학이랑 통계니까~

 

 

 

---

1. 생존분석 Survival Analysis

생존분석(Survival analysis)은 통계학의 한 분야로, 어떠한 현상이 발생하기까지에 걸리는 시간에 대해 분석하는 방법론입니다.

생존분석 Survival Analysis
특정 상태에 존재하는 실험군을 대상으로 특정 조치 treat를 취했을 때, 이에 대한 결과 event가 시간의 변화에 의존적인 경우를 분석하는 것.

관찰하는 시간 내에 관심이 있는 사건 event이 발생하는 모든 자료에 적용할 수 있으며, 해당 사건 event은 '사망'이 아니어도 상관없습니다. 따라서 생존분석은 웹페이지의 고객 이탈률 예측(churn prediction), 설비의 고장 발생 확률 예측(equipment breakdown)에도 다양하게 적용할 수 있습니다.

 

 

 

 

생존분석에는 모수적 방법과 비모수적 방법이 존재합니다.

모수적 방법	준모수적 방법	비모수적 방법
Weibull Exponential Log-logistic Lognormal Generalized Gamma	Cox proportional hazard regression	Kaplan-Meier curve

 

 

모수적 방법이란, 결과 변수가 정규분포, 이항 분포, 포아송 분포 등 사전에 알고 있는 분포를 따른다는 가정하에 회귀분석을 통해 생존 함수를 구축하는 것을 말합니다. 이와는 달리 비모수적 방법은 모집단에 대한 정보가 없어 분포 가정을 적용하지 않고 생존 함수를 구축하는 것을 말합니다.

 

Cox모형은 '생존 시간이 특정한 분포를 따른다' 와 같은 가정이 없다는 점에서 비모수적인 특징을 갖지만, 특정 공변량이 주어졌을 때 hazard function은 baseline hazard function에 공변량을 곱해준 식으로 표현이 가능하다는 점에서 모수적 특징을 갖습니다. 이런 이유로 Cox 모형을 준모수적(semi-parametric model) 이라고 합니다.

 

(이후에 추가로 작성할 포스트에서는 비모수적 방법인 Kaplan-Meier curve와 Cox proportional hazard regression에 대해 정리할 예정입니다.

그전에!!! 생존분석에서 매우 중요한 개념인 중도 절단에 대해 확인해봅시다.)

 

 

 

 

 

---

2. 중도절단 Censored

2.1. 중도절단 개념 Concept of Censored

생존분석을 진행할 때 가장 이상적인 데이터의 조건은 다음과 같습니다.

생존분석 시 이상적인 데이터 조건
    1. 처치 treat가 행해지는 시점이 명확한 데이터.
    2. 모든 참여자들이 관찰기간 내에서 사건 event이 발생하는 데이터.

 

그러나 위의 조건을 만족하지 않고 처치 treat 이후부터 관찰이 종료되는 시점 사이에서 사건 발생 여부를 확인할 수 없는 자료를 중도 절단 Censored 자료라 합니다. 일반적인 통계분석 방법에서는 위의 데이터를 결측 값으로 처리하지만, 생존분석에서는 중도 절단 자료를 포함하여 분석합니다. 중도 절단의 형태로는 우중도 절단(right censoring), 좌중도 절단(left censoring), 구간중도절단(interval censoring) 등이 있습니다. 또한 랜덤 성 여부에 다라 랜덤 중도 절단(random censoring)을 고려할 수 있습니다.

 

중도 절단은 생존 데이터에 대한 우도 함수를 복잡하게 만들어 생존분석 모형을 추정하기 어렵게 하는 경향이 있습니다.

 

임상에서의 중도 절단 Censored 자료
    - Loss to follow up : 환자가 다른 지역으로 이주하여 추적이 불가능
    - Drop out : 환자가 치료를 거부하거나 다른 사유로 치료를 중단
    - Termination of the study : 사건이 발생하기 전에 관찰기간이 종료
    - Death from unrelated cause : 본 연구와 상관없는 다른 이유로 사망

 

 

 

 

중도절단 예시 1)

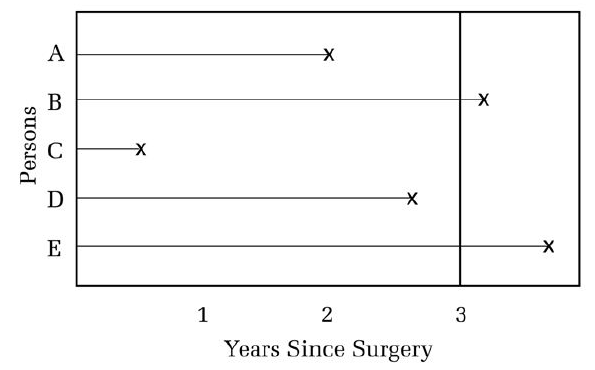
그림1. 중도절단 예시

X로 표시된 부분은 사망시점을 의미한다. 수술 후 3년이 지난 시점이 censoring time이다.

A, C, D는 complete, B, E는 right censored data이다.

 

 

 

 

 

중도 절단 예시 2)

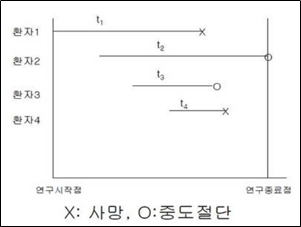
그림2. 중도절단 예시

환자 1 : complete
환자 2 : censored (Termination of the study, right censored)
환자 3 : censored (follow up lose)
환자 4 : complete

만약, 환자 4가 질병에 의한 사망이 아니라 교통사고 등 다른 원인에 의한 사망이라면 censored 처리

 

 

 

 

 

 

 

---

 

2.2. 중도 절단 종류 Type of Censored

2.2.1. 제1유형 우중도 절단

미리 정해놓은 시간에서 실험을 중단하는 경우.

 

2.2.2. 제2유형 우중도 절단

전체 실험 개체들 중 미리 정해놓은 사건 발생률까지 관측 후 중지하는 경우 제2 유형 우중도 절단이 일어납니다.

예를 들어, 모든 실험 개체의 연구 시작 시점이 동일하며 70%가 사건을 가질 경우 관측을 중지한다고 할 때 제2유형 우중도 절단이 일어납니다. => 적당한 비율 r/n(r <n)을 사전에 정해놓고 그에 따라 실험을 중단하는 경우.

전구 수명 실험: 전구 100개 켜놓은 상태에서 5개가 꺼질 때 연구를 종료한다.

 

2.2.3. 임의 우중도 절단

각기 다른 시간에 연구에 참여하고 중도 절단이 일어나는 경우를 임의 우중도 절단이라 합니다. 

 

2.2.4. 구간 중도절단 Interval Censoring

사건이 어떤 구간 내에서 발생하는 경우 구간 중도절단이 일어납니다.

감염 연구에서 환자가 매달 병원에 방문하여 검사를 받는다고 가정한다. 지난달에는 감염이 되지 않았지만 이번 달 방문 시 감염되었다면, 감염이 한 달 사이에 발생했으므로 구간 중도 절단이 된다.

 

2.2.5. 좌중도 절단 Left Censoring

사건event이 연구 시작 이전에 발생하는 경우 좌중도 절단이 일어납니다.

대학생을 대상으로 음주 연구를 위해 처음 음주 시기를 묻는 조사를 실시한다고 가정한다. 대상자가 "언제인지 기억나지 않는다."라고 대답할 경우, 처음 음주 시기를 알 수 없으므로 좌중도 절단이 된다.

 

 

 

 

 

 

 

---

Reference

- 'Survival analysis: Part1-analysis of time-to-event' pdf (link)

- '의학통계 with R, feat. 내과의사' tistory (link)

- [R을 이용한 생존분석 기초] 자유아카데미, 김재희